|
|
(1) |
LE PERDITE DI CARICO
Un fluido in movimento manifesta attrito con le pareti del condotto in cui si trova, i motivi sono i medesimi che si presentano fra due solidi: la scabrezza delle superfici e le forze d’attrazione intermolecolare.
Le conseguenze sono attriti che si oppongono al moto e sottraggono energia al fluido.
Se si escludono variazioni d’altezza e sezione del condotto e s’ipotizza un regime laminare, è immediato ricollegare la perdita ad una diminuzione di pressione, come tra l’altro dimostra il problema di Poiseuille, infatti, in un tubo cilindrico a raggio R e lunghezza L la velocità media è data da:
|
|
(1) |
dove ![]() e
e ![]() sono rispettivamente la pressione d’entrata e d’uscita e m
è la viscosità dinamica che esprime la capacità del fluido di scorrere all’interno del condotto.
sono rispettivamente la pressione d’entrata e d’uscita e m
è la viscosità dinamica che esprime la capacità del fluido di scorrere all’interno del condotto.
Esplicitando nella (1) la variazione di pressione, si ottiene:
|
|
(2) |
sostituendo al raggio il diametro D, la (2) può essere riscritta come:
|
|
(3) |
ricordando poi che il numero di Reynolds vale:
|
|
(4) |
si arriva a:
|
|
(5) |
64 / Re rappresenta il valore che il fattore d’attrito assume nelle condizioni in cui è stato risolto il problema di Poiseuille (in particolare esprime la condizione di regime laminare).
Per rendere la (5) di validità generale è sufficiente sostituire in essa il valore del fattore d’attrito (tradizionalmente indicato con x ) calcolato nel caso in esame.
L’espressione assume quindi la forma:
|
|
(6) |
La (6) risulta di validità generale in quanto x viene calcolato a partire da essa (è cioè definito come il valore che rende vera la relazione).
Per ottenere matematicamente il fattore d’attrito sarebbe necessario tener conto sia dei parametri macroscopici (geometria, rugosità, …) sia di quelli microscopici (natura dei materiali in contatto, forze intermolecolari, …) nel caso specifico considerato.
Il diagramma di Moody
Il problema è evidentemente di grande complessità, inoltre, anche ipotizzando di riuscire a portare a termine il calcolo (obbiettivo che comunque può essere raggiunto solo con strumenti di calcolo numerico), il risultato ottenuto sarebbe significativo unicamente nella particolare situazione presa in esame.
Con una prassi ormai consolidata problemi di questo tipo vengono parametrizzati, in particolare x viene ricavato sperimentalmente in varie condizioni, su tubi di diverse sezioni e con vari fluidi che si muovono a varie velocità, i risultati ottenuti sono rappresentati su quello che è chiamato diagramma di Moody o, in idraulica, arpa di Nikuradse a causa della sua forma caratteristica.
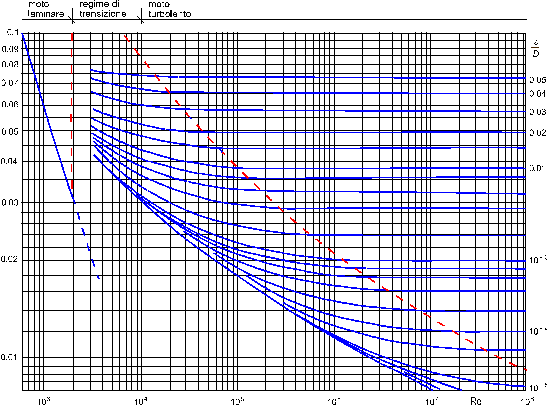 (fig. 1)
(fig. 1)
Il grafico è tracciato con entrambi gli assi in scala logaritmica ed è suddivisibile in quattro regioni distinte.
La prima riporta il valore del fattore d’attrito in regime laminare, cioè per Re < 2300 circa, in questa regione si può assume con buona approssimazione:
|
|
(7) |
La seconda è detta zona critica, si estende per Re compreso fra 2300 e 4000, il regime del fluido dipende fortemente dalla sua natura e dalla geometria del tubo, quest’incertezza si riflette direttamente su x , tanto da non rendere significativi i valori riportati.
La terza, chiamata di transizione turbolenta, ha inizio per valori del numero di Reynolds superiori a 4000, il punto in cui termina è determinato dalla scabrosità relativa (e / D) del mezzo ed è indicata nel grafico da una curva tratteggiata che lo attraversa.
La quarta è caratterizzata dalla fine del regime di transizione e dall’ingresso in quello turbolento, le curve assumono un andamento asintotico, il fattore d’attrito può in questo caso essere approssimato con la relazione:
|
|
(8) |
La lettura del valore di x sul diagramma di Moody può essere fatta una volta conosciuto il valore di scabrezza relativa (la scabrezza di un materiale è ricavabile da tabelle simili a quelle di (tab. 1)), che contraddistingue una particolare curva tracciata, e del numero di Reynolds, semplicemente leggendolo sull’asse delle ordinate.
|
Materiale |
x [mm] |
|
Acciaio chiodato |
0.0 – 9.0 |
|
Cemento |
0.3 – 3.0 |
|
Doghe in legno |
0.19 – 0.9 |
|
Fusione in ferro |
0.25 |
|
Ferro zincato |
0.15 |
|
Acciaio commerciale |
0.046 |
(tab. 1)
Non sempre però è possibile arrivare direttamente ad un valore certo, se infatti la velocità è un’incognita del problema, Re non è conosciuto, ma può essere ricavato a partire dal fattore d’attrito che però dipende a sua volta da Re, il problema si pone naturalmente nella zona critica ed in quella di transizione turbolenta, dove non si conosce una relazione matematica fra x e Re o un’altra grandezza nota.
Per risolvere i problemi a di questo tipo, si deve quindi procedere per tentativi. Assegnato un valore plausibile alla velocità, si calcola il numero di Reynolds (relazione (4)) ed il fattore d’attrito corrispondente attraverso il diagramma di Moody, grazie alla (6) si ricava un nuovo valore di velocità con cui ripetere il procedimento. Le iterazioni terminano quando il risultato ha raggiunto il grado d’approssimazione richiesto (le sue variazioni sono piccole).
Diametro equivalente
La (6) consente a questo punto il calcolo delle perdite di carico in un tubo rettilineo, ma è ancora affetta da limitazioni dovute alle ipotesi fatte, infatti se il tubo non ha sezione circolare, la relazione perde di validità (non ho il valore del diametro D). Per ovviare al problema si introduce il diametro idraulico equivalente, cioè quel valore che è necessario sostituire al posto del fattore D per poter ancora utilizzare la relazione (6). Il fattore sostitutivo è definito da:
|
|
(9) |
dove A è l’area della sezione di tubo e p il suo perimetro, è immediato verificare che per un condotto circolare ![]() .
.
In regime laminare è necessario anche correggere il valore del fattore d’attrito, per questo normalmente si consultano apposite tabelle simili a quella presentata in (tab. 2).
|
Moto laminare |
Moto turbolento |
||
|
Sezione |
|
|
|
|
|
64 |
D |
|
|
|
h / b |
||
|
0.1 |
85 |
1.82 h |
|
|
0.2 |
76 |
1.67 h |
|
|
0.5 |
62 |
1.33 h |
|
|
1.0 |
57 |
1.00 h |
|
|
|
53 |
0.58 h |
|
|
|
96 |
2 h |
|
(tab. 2)
Esercizio
Calcolare le perdite di carico per un condotto con diametro interno D di 2in ed una lunghezza L di 75ft, all’interno scorre ![]() (ammoniaca) ad una temperatura T di 10°
F ed una velocità media w di 70ft/s. La densità del fluido r
è di 0.137
(ammoniaca) ad una temperatura T di 10°
F ed una velocità media w di 70ft/s. La densità del fluido r
è di 0.137![]() mentre la sua viscosità dinamica m
è pari a
mentre la sua viscosità dinamica m
è pari a ![]() . Per la scabrezza del condotto si può assumere un valore e
di 0.00015ft.
. Per la scabrezza del condotto si può assumere un valore e
di 0.00015ft.
Per ottenere un risultato in unità del S.I. è necessario innanzi tutto convertire i valori dati nel problema:
|
1in = 0.0254m |
quindi |
D = 0.0508m |
|
1ft = 0.3048m |
L = 22.86m |
|
|
1lb = 0.4536Kg |
w = 21.3m/s |
|
|
r
= 2.19 |
||
|
m
= |
||
|
e = 0.000046mm |
Risulta necessario ora calcolare il valore assunto dal numero di Reynolds e dalla rugosità relativa:
|
|
|
|
il valore elevato di Re indica che il moto è fortemente turbolento, grazie al diagramma di Moody è ora possibile ricavare il fattore d’attrito:
|
x = 0.0205 |
tramite la relazione (6) si ottiene quindi la perdita di carico cercata:
|
|
La pressione è stata espressa in Pa, unità derivata del S.I., in idraulica tradizionalmente le perdite di carico sono espresse in ![]() (metri di colonna d’acqua), in altre parole quanti metri d’acqua sono necessari per creare una certa pressione. Per effettuare la conversione è sufficiente avvalersi della legge di Stevino:
(metri di colonna d’acqua), in altre parole quanti metri d’acqua sono necessari per creare una certa pressione. Per effettuare la conversione è sufficiente avvalersi della legge di Stevino:
|
p = r × g × h |
sostituiti gli opportuni valori, si ottiene:
|
|
si ha quindi che la pressione calcolata in precedenza è pari a:
|
|
Le perdite di carico concentrate
La relazione (6) permette di calcolare le perdite di carico chiamate distribuite, cioè quelle che avvengono in un tubo rettilineo di sezione costante. Se il condotto presenta però strozzature, angoli o accidentalità di altro tipo è necessario ricorrere ad una diversa relazione che ne tenga conto, la (10) considera appunto queste perdite aggiuntive, dette concentrate, in quanto sono localizzate in un punto preciso del circuito idraulico.
|
|
(10) |
Come si vede la dipendenza dai parametri geometrici del tubo sparisce, così lunghezza e diametro non influiscono più, la relazione complessiva diviene dunque:
|
|
(11) |
I valori del parametro b sono tabulati (un esempio è la (tab. 3)) , è quindi sufficiente sostituirne il valore all’interno dell’equazione per ottenerne la perdita introdotta dall’accidentalità.
|
Accidentalità |
Descrizione |
Valor medio del coefficiente b |
|
|
|
Curva a 90° |
r/d |
|
|
1 |
0.50 |
||
|
2 |
0.35 |
||
|
3 |
0.30 |
||
|
|
Curva a 45° |
r/d |
|
|
1 |
0.35 |
||
|
2 |
0.25 |
||
|
3 |
0.20 |
||
|
|
Giunto a T a 90° |
2 |
|
|
|
Giunto a T a 90° |
a) 0.5 |
|
|
b) 1.5 |
|||
|
|
Giunto a T a 90° |
a) 0.5 |
|
|
b) 1.0 |
|||
|
|
Giunto a T a 90 |
2 |
|
|
|
Giunto a T a 45° |
a) 0.2 |
|
|
b) 1.6 |
|||
|
|
Giunto a T a 45° |
a) 0.3 |
|
|
b) 0.7 |
|||
|
|
Restringimento graduale di sezione |
0.05 |
|
|
|
Restringimento brusco di sezione |
0.5 |
|
|
|
Allargamento brusco di sezione |
1.0 |
|
|
|
Valvola a saracinesca |
chiusura |
|
|
0 |
0.15 |
||
|
¼ |
0.26 |
||
|
½ |
2.06 |
||
|
¾ |
17.00 |
||
|
|
Valvola a 90° |
2 |
|
|
|
Valvola |
1.5 |
|
(tab. 3)
Per un’accidentalità quale un angolo od una valvola la relazione (10) può essere applicata direttamente dopo aver consultato il valore del parametro b nelle tabelle, restringimenti ed allargamenti di sezione presentano invece un’ulteriore difficoltà, infatti, dato che in un condotto la portata in massa rimane costante (cioè tanta acqua entra tanta ne deve uscire), per due punti distinti si può scrivere:
|
|
(12) |
posta S la sezione del tubo, w la velocità del fluido e r la sua densità:
|
|
(13) |
e quindi:
|
|
(14) |
Se inoltre si può formulare l’ipotesi di densità costante (ragionevole per un liquido o per aria che rimane a pressione quasi costante, non certo per un gas pressurizzato che fuoriesce da una bomboletta), l’equazione assume la forma:
|
|
(15) |
risulta evidente che la velocità aumenta al diminuire della sezione (e viceversa), è quindi necessario prestare attenzione su quale valore sostituire nella (10), se cioè il parametro b che s’intende utilizzare è riferito a monte o a valle dell’accidentalità. Sotto le ipotesi fatte per ricavare la (15) risulta ugualmente abbastanza semplice calcolare con essa la velocità cercata.
Lunghezza equivalente
Nei circuiti idraulici è possibile tener conto delle accidentalità anche variando la lunghezza del condotto, ovvero sommando al parametro L un parametro ![]() calcolato in modo che tutte le perdite appaiano distribuite. La (11) assume quindi una forma alternativa:
calcolato in modo che tutte le perdite appaiano distribuite. La (11) assume quindi una forma alternativa:
|
|
(16) |
Ogni accidentalità possiede un proprio valore di lunghezza equivalente che non viene ricavato da tabelle, ma da un grafico chiamato normogramma (fig. 2).
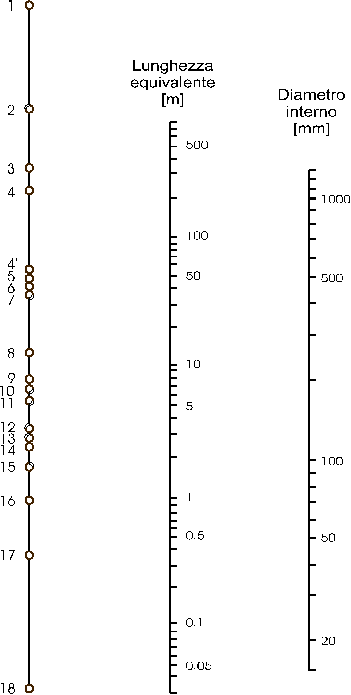
(fig .2)
|
Punto |
Accidentalità |
Punto |
Accidentalità |
|
1 |
Saracinesca aperta ¼" |
10 |
Allargamento di sezione 1® 4 |
|
2 |
Valvola dritta aperta |
11 |
Raccordo curvo a 90° raggio medio |
|
3 |
Saracinesca aperta ½" |
12 |
Raccordo curvo a 90° raggio largo |
|
4 |
Valvola ad angolo aperta |
13 |
Allargamento di sezione 1® 2 |
|
4’ |
Filtro |
14 |
Imbocco |
|
5 |
Valvola di ritegno aperta |
15 |
Raccordo curvo a 45° |
|
6 |
Raccordo curvo a 180° |
16 |
Restringimento di sezione 4® 1 |
|
7 |
Raccordo a squadra a 90° |
17 |
Saracinesca aperta 1" |
|
8 |
Saracinesca aperta ¾" |
18 |
Saracinesca aperta 2" |
|
9 |
Raccordo curvo a 90° raggio stretto |
(tab. 3)
Il diagramma viene presentato con una tabella indispensabile per il calcolo della lunghezza equivalente cercata. Una volta stabilito il tipo di accidentalità, grazie alla tabella si congiunge il punto corrispondente sull’asse sinistro del grafico con il valore del diametro interno del condotto riportato sull’asse destro, l’intersezione con la linea centrale determina il valore correttivo da sommare alla lunghezza del circuito.
Ad esempio per un filtro (punto 4’) ed un diametro interno di 100mm si ottiene una lunghezza equivalente di circa 10m.