
Explicit Ambix formulas for High Order Ambisonics
|
The goal of this page is to provide an univoque, explicit set of formulas describing the amplitude of the Ambisonics polar patterns as function of the azimuth and elevation angles, and also as a function of the three cartesian coordinates of the unit vector pointing towards the sound source.
Unfortunately in the years many different Ambisonics formulations have been employed, differing in naming, channel order, and gain normalization.
Furthermore, the Cartesian and Spherical coordinate systems have also been messed up, again with wrong naming, polarity inversion, and so on.
So this page also serves for providing the correct information about all these possible causes of errors.
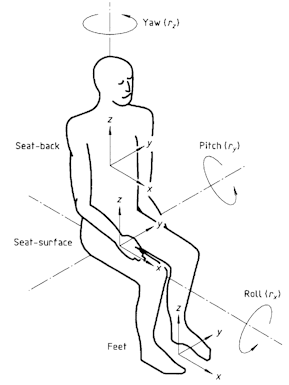
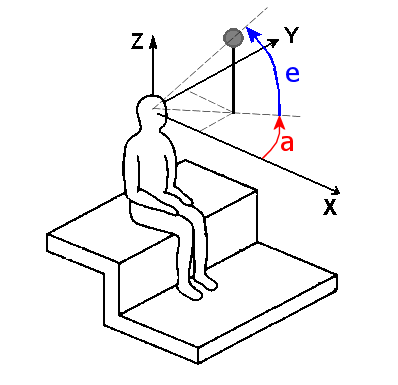
The Cartesian reference must be conforming to ISO standards (for example, ISO2631-1:1997), as in the following pictures (the left one is taken directly from the ISO 2631-1:1997 standard):



The spherical coordinate system is coherent with this Cartesian reference system: the azimuth angle (a) lies in the XY plane, starting form the X axis and running towards the Y axis, so an azimut of 0 degrees means "Front", 90 degrees means "Left", 180 degrees means "Back" and -90 degrees (which also equates to 270 degrees) means "Right". Elevation angle (e) is measured from the horizontal plane, with positive elevations going up to the sky, so e = 90 degrees means Zenith (or North pole) and e=-90 degrees means Nadir (or South pole).
The usage of other symbols for azimuth and elevation must be discouraged. Many people use θ (theta) and j (phi) for naming azimuth and elevation, but these are often swapped (there is no univoque correspondance establishing if theta is azimuth or elevation), and in some cases the value of elevation is not starting from the horizontal plane, but instead from the North pole and going down, as shown, for example, on the Wikipedia page https://en.wikipedia.org/wiki/Spherical_coordinate_system, where the two possible naming conventions are shown, but elevation is always wrong.
Also the sign of azimuth is sometimes reversed: for example, in FB360 Spatial Workstation the elevation angle is correct, but the azimut is reversed, with positive values going right instead of going left, as it should be. The same problem occurs in Audio Ease and Ambix plugin suites.
Luckily enough, most other software used for creating and manipulating High Order Ambisonics signals are usually perfectly coherent with the ISO 2631 standard adopted here, for example O3A, Noise Makers, Wigware, Ambdec, York University, Ambisonic Studio, Gerzonic, etc.
I hope that the information above serves for avoiding errors... And perhaps the authors of software employing wrong conventions cited above will decide to fix their crappy angular systems...
And now let's define the spherical harmonics functions, which provide the direction-dependent gain of each of the Ambisonics signals.
These functions are defined in a series, with 2 more functions for each order, providing an increasing spatial resolution. The following figure shows these direction-dependent gain functions up to 7th order:
The meaning of the colors is the following:
RED means positive
BLUE means negative
And finally here we present the explicit formulas giving these gain functions, either in polar and Cartesian coordinates, worked out from the formulas given here, and corresponding to current standard Ambix format (that is, channel ordering is ACN and gain normalization is SN3D - any other convention is nowadays obsolete and should be completely avoided):
|
ACN |
Order |
Name |
Image |
Azimuth/Elevation Representation |
Cartesian Representation |
|
0 |
0 |
W |
|
1 |
1 |
|
1 |
1 |
Y |
|
sin(a)*cos(e) |
y |
|
2 |
1 |
Z |
|
sin(e) |
z |
|
3 |
1 |
X |
|
cos(a)*cos(e) |
x |
|
4 |
2 |
V |
|
sqrt(3/4)*sin(2*a)*(cos(e))^2 |
sqrt(3)*x*y |
|
5 |
2 |
T |
|
sqrt(3/4)*sin(a)*sin(2*e) |
sqrt(3)*y*z |
|
6 |
2 |
R |
|
(1/2)*(3*(sin(e))^2-1) |
(1/2)*(3*z^2-1) |
|
7 |
2 |
S |
|
sqrt(3/4)*cos(a)*sin(2*e) |
sqrt(3)*x*z |
|
8 |
2 |
U |
|
sqrt(3/4)*cos(2*a)*(cos(e))^2 |
sqrt(3/4)*(x^2-y^2) |
|
9 |
3 |
Q |
|
sqrt(5/8)*sin(3*a)*(cos(e))^3 |
sqrt(5/8)*y*(3*x^2-y^2) |
|
10 |
3 |
O |
|
sqrt(15/4)*sin(2*a)*sin(e)*(cos(e))^2 |
sqrt(15)*x*y*z |
|
11 |
3 |
M |
|
sqrt(3/8)*sin(a)*cos(e)*(5*(sin(e))^2-1) |
sqrt(3/8)*y*(5*z^2-1) |
|
12 |
3 |
K |
|
(1/2)*sin(e)*(5*(sin(e))^2-3) |
(1/2)*z*(5*z^2-3) |
|
13 |
3 |
L |
|
sqrt(3/8)*cos(a)*cos(e)*(5*(sin(e))^2-1) |
sqrt(3/8)*x*(5*z^2-1) |
|
14 |
3 |
N |
|
sqrt(15/4)*cos(2*a)*sin(e)*(cos(e))^2 |
sqrt(15/4)*z*(x^2-y^2) |
|
15 |
3 |
P |
|
sqrt(5/8)*cos(3*a)*(cos(e))^3 |
sqrt(5/8)*x*(x^2-3*y^2) |
|
16 |
4 |
|
sqrt(35/64)*sin(4*a)*(cos(e))^4 |
sqrt(35/4)*x*y*(x^2-y^2) |
|
|
17 |
4 |
|
sqrt(35/8)*sin(3*a)*sin(e)*(cos(e))^3 |
sqrt(35/8)*y*z*(3*x^2-y^2) |
|
|
18 |
4 |
|
sqrt(5/16)*sin(2*a)*(cos(e))^2*(7*(sin(e))^2-1) |
sqrt(5/4)*x*y*(7*z^2-1) |
|
|
19 |
4 |
|
sqrt(5/32)*sin(a)*sin(2*e)*(7*(sin(e))^2-3) |
sqrt(5/8)*y*z*(7*z^2-3) |
|
|
20 |
4 |
|
1/8*(35*sin(e)^4-30*sin(e)^2+3) |
1/8*(35*z^4-30*z^2+3) |
|
|
21 |
4 |
|
sqrt(5/32)*cos(a)*sin(2*e)*(7*(sin(e))^2-3) |
sqrt(5/8)*x*z*(7*z^2-3) |
|
|
22 |
4 |
|
sqrt(5/16)*cos(2*a)*(cos(e))^2*(7*(sin(e))^2-1) |
sqrt(5/16)*(x^2-y^2)*(7*z^2-1) |
|
|
23 |
4 |
|
sqrt(35/8)*cos(3*a)*sin(e)*(cos(e))^3 |
sqrt(35/8)*x*z*(x^2-3*y^2) |
|
|
24 |
4 |
|
sqrt(35/64)*cos(4*a)*(cos(e))^4 |
sqrt(35/64)*(x^4-6*x^2*y^2+y^4) |
|
|
25 |
5 |
|
sqrt(63/128)*sin(5*a)*(cos(e))^5 |
sqrt(63/128)*y*(5*x^4-10*x^2*y^2+y^4) |
|
|
26 |
5 |
|
sqrt(315/64)*sin(4*a)*sin(e)*(cos(e))^4 |
sqrt(315/4)*x*y*z*(x^2-y^2) |
|
|
27 |
5 |
|
sqrt(35/128)*sin(3*a)*(cos(e))^3*(9*(sin(e))^2-1) |
sqrt(35/128)*y*(y^4-2*x^2*y^2-3*x^4-8*y^2*z^2+24*x^2*z^2) |
|
|
28 |
5 |
|
sqrt(105/16)*sin(2*a)*sin(e)*(cos(e))^2*(3*(sin(e))^2-1) |
sqrt(105/4)*x*y*z*(2*z^2-x^2-y^2) |
|
|
29 |
5 |
|
sqrt(15/64)*sin(a)*cos(e)*(21*(sin(e))^4-14*(sin(e))^2+1) |
sqrt(15/64)*y*(x^4+2*x^2*y^2+y^4-12*x^2*z^2-12*y^2*z^2+8*z^4) |
|
|
30 |
5 |
|
1/8*(63*(sin(e))^5-70*sin(e)^3+15*sin(e)) |
1/8*z*(63*z^4-70*z^2+15) |
|
|
31 |
5 |
|
sqrt(15/64)*cos(a)*cos(e)*(21*(sin(e))^4-14*(sin(e))^2+1) |
sqrt(15/64)*x*(x^4+2*x^2*y^2+y^4-12*x^2*z^2-12*y^2*z^2+8*z^4) |
|
|
32 |
5 |
|
sqrt(105/16)*cos(2*a)*sin(e)*(cos(e))^2*(3*(sin(e))^2-1) |
sqrt(105/16)*z*(2*x^2*z^2-2*y^2*z^2-x^4+y^4) |
|
|
33 |
5 |
|
sqrt(35/128)*cos(3*a)*(cos(e))^3*(9*(sin(e))^2-1) |
sqrt(35/128)*x*(2*x^2*y^2+8*x^2*z^2-24*y^2*z^2-x^4+3*y^4) |
|
|
34 |
5 |
|
sqrt(315/64)*cos(4*a)*sin(e)*(cos(e))^4 |
sqrt(315/64)*z*(x^4-6*x^2*y^2+y^4) |
|
|
35 |
5 |
|
sqrt(63/128)*cos(5*a)*(cos(e))^5 |
sqrt(63/128)*x*(x^4-10*x^2*y^2+5*y^4) |
|
|
36 |
6 |
|
1/16*sqrt(231/2)*sin(6*a)*(cos(e))^6 |
1/8*sqrt(231/2)*x*y*(3*x^4-10*x^2*y^2+3*y^4) |
|
|
37 |
6 |
|
3/8*sqrt(77/2)*sin(5*a)*sin(e)*(cos(e))^5 |
3/8*sqrt(77/2)*y*z*(5*x^4-10*x^2*y^2+y^4) |
|
|
38 |
6 |
|
3/16*sqrt(7)*sin(4*a)*(cos(e))^4*(11*(sin(e))^2-1) |
3/4*sqrt(7)*x*y*(-x^4+y^4 +10*x^2*y^2-10*y^2*z^2) |
|
|
39 |
6 |
|
1/8*sqrt(105/2)*sin(3*a)*sin(e)*(cos(e))^3*(11*(sin(e))^2-3) |
1/8*sqrt(105/2)*y*z*(-9*x^4+3*y^4-6*x^2*y^2+24*x^2*z^2-8*y^2*z^2) |
|
|
40 |
6 |
|
1/16*sqrt(105/2)*sin(2*a)*(cos(e))^2*(33*(sin(e))^4-18*(sin(e))^2+1) |
1/8*sqrt(105/2)*x*y*(x^4+y^4+16*z^4+2*x^2*y^2-16*x^2*z^2-16*y^2*z^2) |
|
|
41 |
6 |
|
1/16*sqrt(21)*sin(a)*sin(2*e)*(33*(sin(e))^4-30*(sin(e))^2+5) |
1/8*sqrt(21)*y*z*(5*x^4+5*y^4+8*z^4+10*x^2*y^2-20*x^2*z^2-20*y^2*z^2) |
|
|
42 |
6 |
|
1/16*(231*(sin(e))^6-315*(sin(e))^4+105*(sin(e))^2-5) |
1/16*(231*z^6-315*z^4+105*z^2-5) |
|
|
43 |
6 |
|
1/16*sqrt(21)*cos(a)*sin(2*e)*(33*(sin(e))^4-30*(sin(e))^2+5) |
1/8*sqrt(21)*x*z*(5*x^4+5*y^4+8*z^4+10*x^2*y^2-20*x^2*z^2-20*y^2*z^2) |
|
|
44 |
6 |
|
1/16*sqrt(105/2)*cos(2*a)*(cos(e))^2*(33*(sin(e))^4-18*(sin(e))^2+1) |
1/16*sqrt(105/2)*(x^6-y^6+x^4*y^2-x^2*y^4-16*x^4*z^2+16*x^2*z^4+16*y^4*z^2-16*y^2*z^4) |
|
|
45 |
6 |
|
1/8*sqrt(105/2)*cos(3*a)*sin(e)*(cos(e))^3*(11*(sin(e))^2-3) |
1/8*sqrt(105/2)*x*z*(-3*x^4+6*x^2*y^2+8*x^2*z^2-24*y^2*z^2+9*y^4) |
|
|
46 |
6 |
|
3/16*sqrt(7)*cos(4*a)*(cos(e))^4*(11*(sin(e))^2-1) |
3/16*sqrt(7)(-x^6+5*x^4*y^2 +10*x^4*z^2+5*x^2*y^4+10**y^4*z^2-y^6-60*x^2*y^2*z^2) |
|
|
47 |
6 |
|
3/8*sqrt(77/2)*cos(5*a)*sin(e)*(cos(e))^5 |
3/8*sqrt(77/2)*x*z*(5*y^4-10*x^2*y^2+x^4) |
|
|
48 |
6 |
|
1/16*sqrt(231/2)*cos(6*a)*(cos(e))^6 |
1/16*sqrt(231/2)*(x^6-15*x^4*y^2+15*x^2*y^4-y^6) |
|
|
49 |
7 |
|
1/32*sqrt(429)*sin(7*a)*(cos(e))^7 | ||
|
50 |
7 |
|
1/16*sqrt(3003/2)*sin(6*a)*sin(e)*(cos(e))^6 | ||
|
51 |
7 |
|
1/32*sqrt(231)*sin(5*a)*(13*(sin(e))^2-1)*(cos(e))^5 | ||
|
52 |
7 |
|
1/16*sqrt(231)*sin(4*a)*(13*(sin(e))^3-3*sin(e))*(cos(e))^4 | ||
|
53 |
7 |
|
1/32*sqrt(21)*sin(3*a)*(143*(sin(e))^4-66*(sin(e))^2+3)*(cos(e))^3 | ||
|
54 |
7 |
|
1/16*sqrt(21/2)*sin(2*a)*(143*(sin(e))^5-110*(sin(e))^3+15*sin(e))*(cos(e))^2 | ||
|
55 |
7 |
|
1/32*sqrt(7)*sin(a)*(429*(sin(e))^6-495*(sin(e))^4+135*(sin(e))^2-5)*cos(e) | ||
|
56 |
7 |
|
1/16*(429*(sin(e))^7-693*(sin(e))^5+315*(sin(e))^3-35*sin(e)) | ||
|
57 |
7 |
|
1/32*sqrt(7)*cos(a)*(429*(sin(e))^6-495*(sin(e))^4+135*(sin(e))^2-5)*cos(e) | ||
|
58 |
7 |
|
1/16*sqrt(21/2)*cos(2*a)*(143*(sin(e))^5-110*(sin(e))^3+15*sin(e))*(cos(e))^2 | ||
|
59 |
7 |
|
1/32*sqrt(21)*cos(3*a)*(143*(sin(e))^4-66*(sin(e))^2+3)*(cos(e))^3 | ||
|
60 |
7 |
|
1/16*sqrt(231)*cos(4*a)*(13*(sin(e))^3-3*sin(e))*(cos(e))^4 | ||
|
61 |
7 |
|
1/32*sqrt(231)*cos(5*a)*(13*(sin(e))^2-1)*(cos(e))^5 | ||
|
62 |
7 |
|
1/16*sqrt(3003/2)*cos(6*a)*sin(e)*(cos(e))^6 | ||
|
63 |
7 |
|
1/32*sqrt(429)*cos(7*a)*(cos(e))^7 | ||
The original N3D formulas are here:
Original Formulas for High order Ambisonics (ACN N3D format up to 7th order)
If you find errors in these formulas, please point them out to the author of this page...
Angelo Farina, August 2017 - September 2022